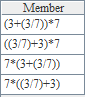esProc can process big text files conveniently by providing cursor data object. The following example is to illustrate this.
Let’s assume that there is a text file, sales.txt, with ten million sales records. Its main fields include SellerID, OrderDate and Amount. Now compute each salesman’s total Amount of big orders in the past four years. The big orders refer to those whose amount is above 2000.
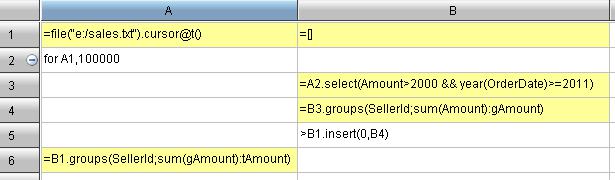
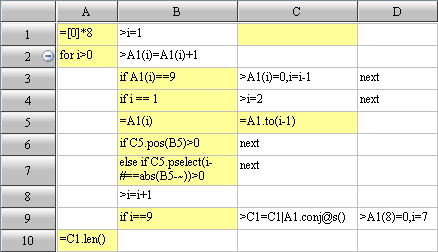
esProc code:
Code interpretation:
A1: If all the ten million records are read into memory simultaneously, memory will overflow. So the job will be done in batches.
A2: Read by looping, 100,000 rows at a time.
B3: Filter each batch of data, select those records whose amount is above 2000 after the year of 2011.
B4: Group and summarize the filtered data, seek the sales of each salesperson in this batch of data.
B5: Add the computed result of this batch of data to a certain variable (B1), and move on to the computation of next batch of data.
B6: After all the computations, sales of each salesperson in every batch of data will be found in B1. Last, group and summarize these sales data and seek each salesperson’s total sales amount.
Analysis:
In cell A1, esProc cursor is created with function cursor. The cell name is the cursor’s variable name. When the cursor is created, data will not be read in the memory directly. Read-in will only be executed while fetch operation or other equal operations are going on, e.g., the code for A1,100000 in cell A2 represents reading data from cursor by looping with 100,000 rows at a time. We can see that the data size in memory is always kept in a relatively small level and no overflows will occur.
select and groups are computation functions specially used with structured data. After the data is read in the memory with esProc cursor, they can be processed and analyzed by employing functions of professional structured data computation library. This is more convenient than writing underlying code by hand.
Equipped with functions and grammar of semi-structured data processing, e.g., function for data split and merging, looping and traversal statement and branch judgment statement, esProc cursor can do complex task of data cleansing and arrangement and form easily computed structured data.
Splitting and analyzing
For instance, the format of weblog is too complex to be computed and analyzed directly. A typical web blog text need to be transformed into a two-dimensional table of standard format in order to be used in structured data computation or be stored in a database.
A record in the original weblog:
- 10.10.10.145 - - [01/May/2013:03:24:56 -0400] "GET /product/p0040001/review.jsp?page=5 HTTP/1.1" 200 8100 "http://www.xxx.com/xxxx.html""Mozilla/5.0 (Windows NT 6.1) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/29.0.1547.66 Safari/537.36" 0 tankLee in 9fc0792eb272b78916c3872e9ad –
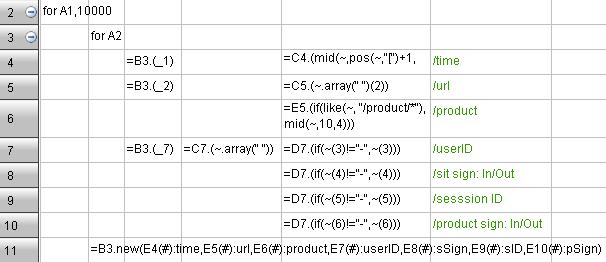
Time | url | product | userID | sSign | sID | pSign |
|---|---|---|---|---|---|---|
01/May/2013:03:24:56 | /product/p0040001/review.jsp?page=5 | p0040001 | tankLee | In | 9fc0792eb272b78916c3872e9ad |
The following case omits the process of file accesses and the final merging of multiple batches of data(refer to the previous example), and lists the code for splitting and analyzing directly.
Data cleansing
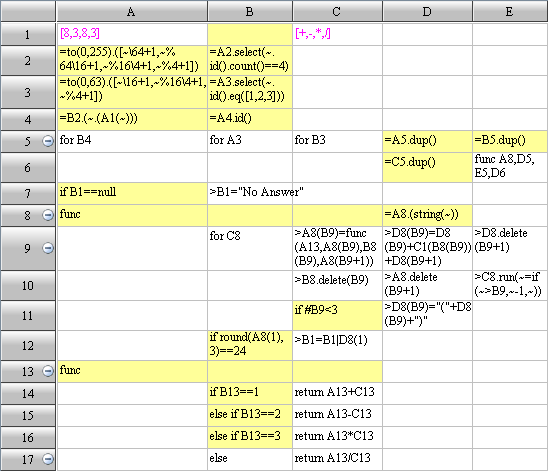
Let’s see a typical example of data cleansing. Since the employee table read in from a file is not a standard format, it need to be reorganized into standard structural data in batches. Data of the current batch will be stored in cell D3 temporarily. The rule for reorganizing is:
- The record is invalid if UserID and firstName is null or blank string.
- UserID can only contain digits; the record is invalid if letters appear in it.
- For repeated UserID, only the last entered record is kept.
- Delete possible spacing before and after the data.
- Capitalize all the first letters of firstName.
- Full name is combined in the form of firstName+”.”+”lastName”. But, if lastName is null or blank string, fullname equals to firstName.
The following table also omits the process of file accesses and the merging of multiple batches of data, and only lists the code for data cleansing: